[toc]
python高阶函数和装饰器二

练习
1. 把一个字典扁平化
- 源字典
{'a':{'b':1,'c':2},'d':{'e':3,'f':{'g':4}}}
#!/usr/bin/env python
source = {'a':{'b':1,'c':2},'d':{'e':3,'f':{'g':4}}}
target = {}
def flatmap(src,prefix=''):
for k,v in src.items():
if isinstance(v,(list,tuple,set,dict)):
flatmap(v,prefix=prefix+k+'.')
else:
target[prefix+k] =v
flatmap(source)
print(target)
# 输出
{'a.b': 1, 'a.c': 2, 'd.e': 3, 'd.f.g': 4}
- 方法二
source = {'a':{'b':1,'c':2},'d':{'e':3,'f':{'g':4}}}
def flatmap(src,dest=None,prefix=''):
if dest == None:
dest = {}
for k,v in src.items():
if isinstance(v,(list,tuple,set,dict)):
flatmap(v,dest,prefix=prefix+k+'.')
else:
dest[prefix+k] = v
return dest
print(flatmap(source))
- 能否不暴露给外界内部的字典呢 ?
- 能否函数就提供一个参数源字典,返回一个新的扁平化字典呢 ?
- 递归的时候要把目录字典的引用传递多层,怎么处理?
即: 方法三
source = {'a':{'b':1,'c':2},'d':{'e':3,'f':{'g':4}}}
def flatmap(src):
def _flatmap(src,dest=None,prefix=''):
for k,v in src.items():
key = prefix + k
if isinstance(v,(list,tuple,set,dict)):
_flatmap(v,dest,key + '.')
else:
dest[key] = v
dest = {}
_flatmap(src,dest)
return dest
print(flatmap(source))
# 输出
{'a.b': 1, 'a.c': 2, 'd.e': 3, 'd.f.g': 4}
2. 实现Base64编码
要求自己实现算法,不用库
说明:
将输入每3个字节断开,拿出一个3个字节,每6个bit断开成4段;
2**6 = 64,因此有了base64的编码表;
每一段当一个8big看它的值,这个值就是Base64编码表的索引值,找到对应字符;
再取3个字节,同样处理,直到最后。
举例:
abc对应原ASCII码为: 0x610 0x620 0x63
01100001 01100010 011000011 # abc
011000 010110 001001 100011
000111000 00010110 0001001 00100011 # 每6位补齐为8位
未尾的处理?
1、 正好3个字节,处理方式同上;
2、 剩1个字节或2个字节,用0满补3个字节;
3、 补0的的字节用=表示;
实现代码
#!/usr/bin/env python
# 自已实现对一段字符串进行base64编码
alphabet = b"ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/"
teststr = "abcd"
#teststr ="ManMa"
def base64(src):
ret = bytearray()
length = len(src)
# r记录补0的个数
r = 0
for offset in range(0,length,3):
if offset + 3 <= length:
triple = src[offset:offset+3]
else:
triple = src[offset:]
r = 3 - len(triple)
triple = triple + '\x00' * r # 补几个0
# print(triple,r)
# 将3个字节看成一个整体转成字节bytes, 大端模式
# abc => 0x616263
b = int.from_bytes(triple.encode(),'big') #小端模式为'little'
print(hex(b))
# 011000001 011000010 01100011 # abc
# 011000 010110 001001 100011 # 每6位断开
for i in range(18, -1, -6):
if i == 18:
index = b >> i
else:
index = b >> i & 0x3F #0b0011 1111
# 得到base64编码的列表
ret.append(alphabet[index])
# 策略是不管是不是补零,都填满, 只有最后一次可能出现补零的;
# 在最后替换掉就是了,代码清晰,而且替换至多2次;
# 在上一个循环中判断 r!=0,效率可能会高些;
for i in range(1, r+1): # 1到r,补几个0替换几个=
ret[-i] = 0x3D
return bytes(ret)
print(base64(teststr))
import base64
print(base64.b64encode(teststr.encode()))
# 输出
0x616263
0x640000
b'YWJjZA=='
b'YWJjZA=='
3. 求2个字符串的最长公共子串
思考:
s1 = 'abcdefg's2 = 'defabcd'
可不可以这样思考?
字符串都是连续的字符,所以才有了下面的思路。
思路一:
第一轮
从s1中依次取1个字符,在s2查找,看是否能够找到子串;
如果没 一个字符在s2中找到,说明就没有公共子串,直接退出。如果找到了至少一个公共子串,则很有可能还有更长的公共子串,可以进入下一轮;
第二轮
然后从s1中取连续的2个字符,在s2中找,看看能否找到公共的子串。如果没找到,说明最大公共子串就是上一轮的随便的一个就行了。如果找到至少一个,则说明公共子串可能还可以再长一些。可进入下一轮;
改进,其实只要找到第一轮的公共子串的索引,最长公共子串也是从它开始的,所以以后的轮次都从这些索引位置开始,可以减少比较的次数;
思路二:
既然是求最大的字串,我先看s1全长作为子串;
在s2中搜索,是否返回正常的index, 正常就找到了最长子串。
没有找到,把s1按照 length-1取多个子串;
在s2中搜索,是否能返回正常的index。
注意:
不要一次把s1的所有子串生成,用不了,也不要从最短开始,因为题目要最长的;
但是也要注意,万一他们公共子串就只有一个字符,或者很少字符的,思路就一就会占优势。
#!/usr/bin/env python
s1 = 'abcdefg'
s2 = 'defabcdoabcdeftw'
s3 = '1234a'
def findit(str1,str2):
count = 0# 看看效率,计数;
length = len(str1)
for sublen in range(length,0, -1):
for start in range(0, length - sublen +1):
substr = str1[start:start + sublen]
count +=1
if str2.find(substr) > -1: # found
print("count={}, substrlen={}".format(count,sublen))
return substr
print(findit(s1,s2))
print(findit(s1,s3))
# 输出
count=2, substrlen=6
abcdef
count=22, substrlen=1
a
让s2的每一个元素,去分别和s2的每一个元素比较,相同就是1,不同就是0,有下面的矩阵;
| S1 | |
|---|---|
| S1 | 0001000 |
| S1 | 0000100 |
| S1 | 0000010 |
| S1 | 1000000 |
| S1 | 0010000 |
| S1 | 0001000 |
上面都是s1的索引
看与斜对角线平行的线,这个线是穿过1的,那么最长的就是最长子串;
print(s1[3:3+3])
print(s1[0:0+4])最长
矩阵求法还fdms一个字符扫描最子子串的过程,扫描的过程就是len(s1) len(s2)次,0(nm)
有办法一遍循环就找出最长的子串吗?0001000第一行,索引为3,0;
第二行的时候如果4,1是1,就判断3,0是否为1,为1就把3,0加1;
第二行的进修如果5,2是1,就判断4,1是否为1,是1就加1,再就判断3,0是否为1,为1就把3,0加1;
| S1 | |
|---|---|
| s1 | 0003000 |
| s1 | 0000200 |
| s1 | 0000010 |
| s1 | 4000000 |
| s1 | 0300000 |
| s1 | 0020000 |
| s1 | 0001000 |
上面的方法是个递归问题,不好。
最后在矩阵中找到最大的元素,从它开始就能写出最长的子串了。
但是这个不好算,因为是逆推的,改为顺推。
| s1 | |
|---|---|
| S1 | 0001000 |
| s1 | 0000200 |
| s1 | 0000030 |
| s1 | 1000000 |
| s1 | 0200000 |
| s1 | 0030000 |
| s1 | 0004000 |
顺推的意思,就是如果找到一个就看前一个的数字是几,然后在它的基础上加1。
s1 = 'abcdefg'
s2 = 'defabcd'
s2 = 'defabcdoabcdeftw'
s3 = '1234a'
s4 = '5678'
def findit(str1,str2):
matrix = []
# 从x轴或者y轴取都可以,选择x轴,xmax和xindex
xmax = 0
xindex = 0
for i,x in enumerate(str2):
matrix.append([])
for j,y in enumerate(str1):
if x !=y :
matrix[i].append(0)
else:
if x == 0 or y ==0: # 在边上
matrix[i].append(1)
else: # 不在边上
matrix[i].append(matrix[i-1][j-1]+1)
if matrix[i][j] > xmax: # 判断当前加入的值和记录的最大值比较
xmax = matrix[i][j]# 记录最大值,用于下次比较
xindex = j # 记录当前值的x轴偏移量
xindex += 1 # 切片的时候不包,因此+1
return str1[xindex - xmax: xindex]# xmax 正好是子串的长度
print(findit(s1,s2))
print(findit(s1,s3)) #a
print(findit(s1,s4)) #空串
# 输出
abcdef
a
Python树的遍历和堆排序
二叉树的遍历
- 遍历: 迭代所有元素一遍;
树的遍历: 对树中的所有元素不重复地访问一遍,也称作扫描;
广度优先遍历
- 层序遍历
- 深度优先遍历
- 前序遍历
- 中序遍历
- 后序遍历
遍历序列: 将树中的所有元素遍历一遍后,得到的无素的序列。将层次结构转换成了线性结构;
层序遍历
- 按照树的层次,从第一层开始,自左向右的遍历元素;
遍历序列
ABCDEFGHI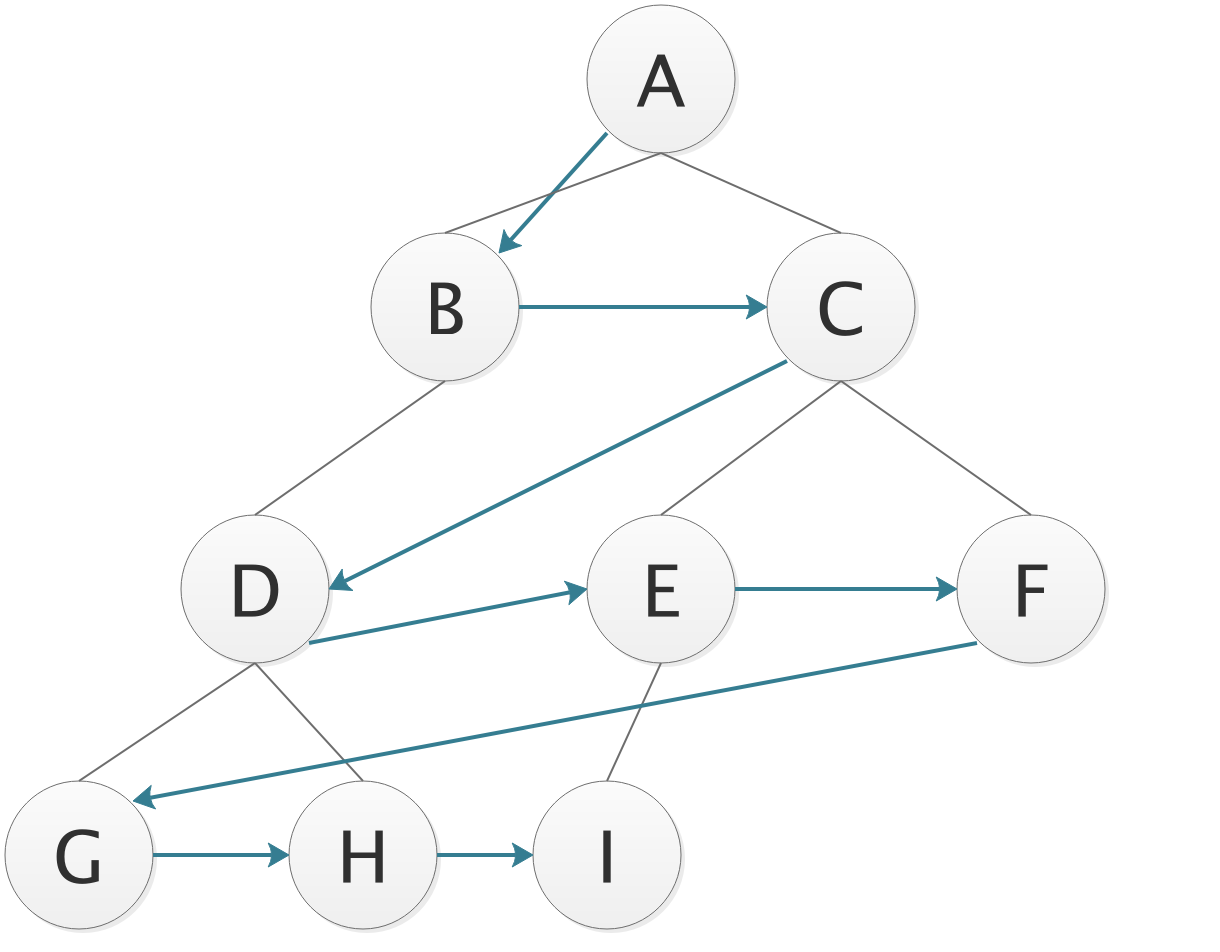
- 深度优先遍历
- 设树的根结点为D,左子树为L,右子树为R,且要求L一定在R之前,则有下面几种遍历方式:
- 前序遍历,也叫先序遍历,也叫先根遍历,DLR;
- 中序遍历,也叫中根遍历, LDR;
- 后序遍历,也叫后根遍历,LRD;
二叉树的遍历
- 前序遍历DLR
- 从根结点开始,先左子树后右子树;
- 每个子树内部依然是先根结点,再左子树后右子树,递归遍历;
- 遍历序列;
A BDGH CEIF
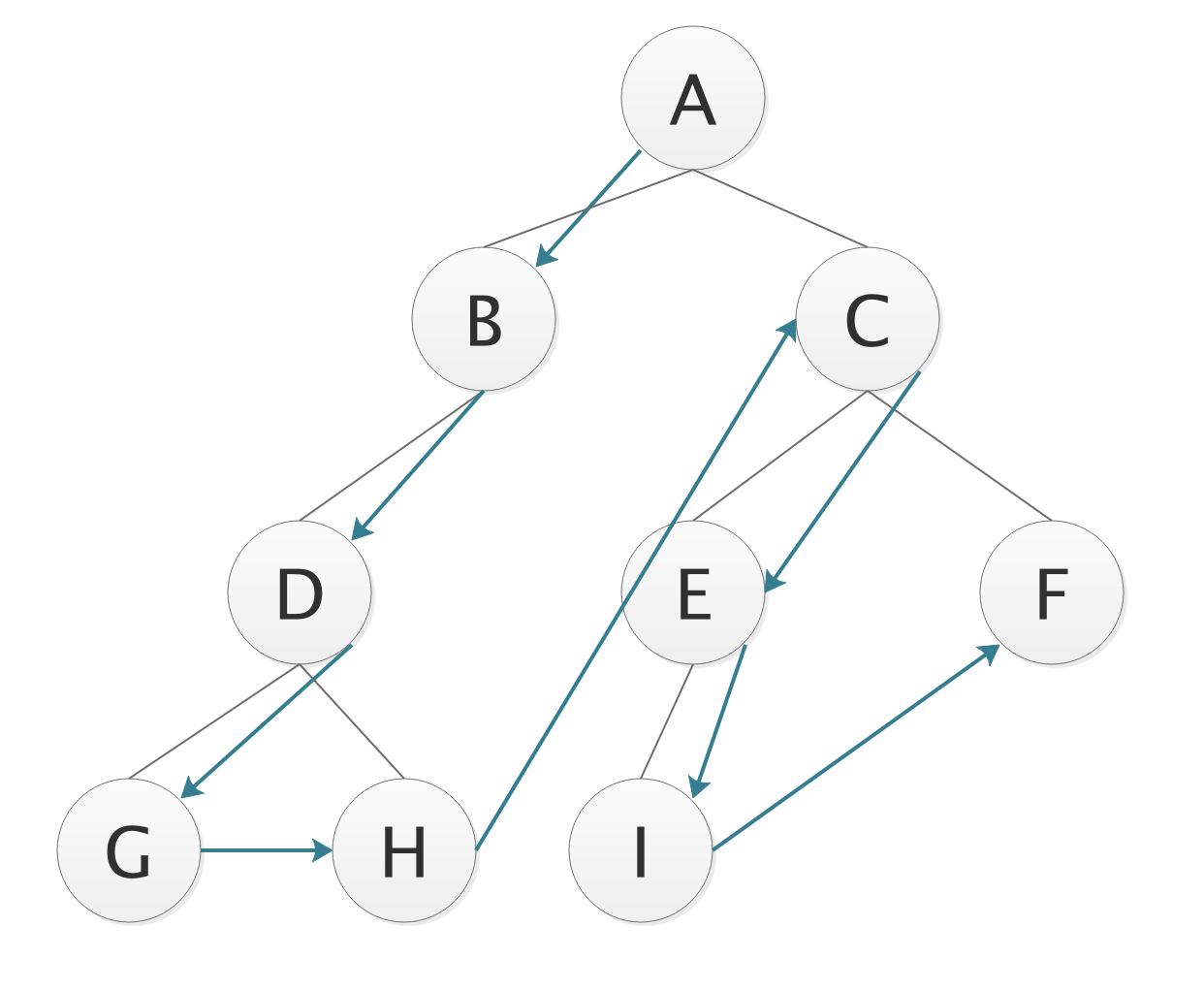
- 中序遍历LDR
- 从根结点的左子树开始遍历,然后是根结点,再右子树;
- 每个子树内部,也是先左子树,后根结点,再右子树。递归遍历;
- 遍历序列;
GDHB A IECF
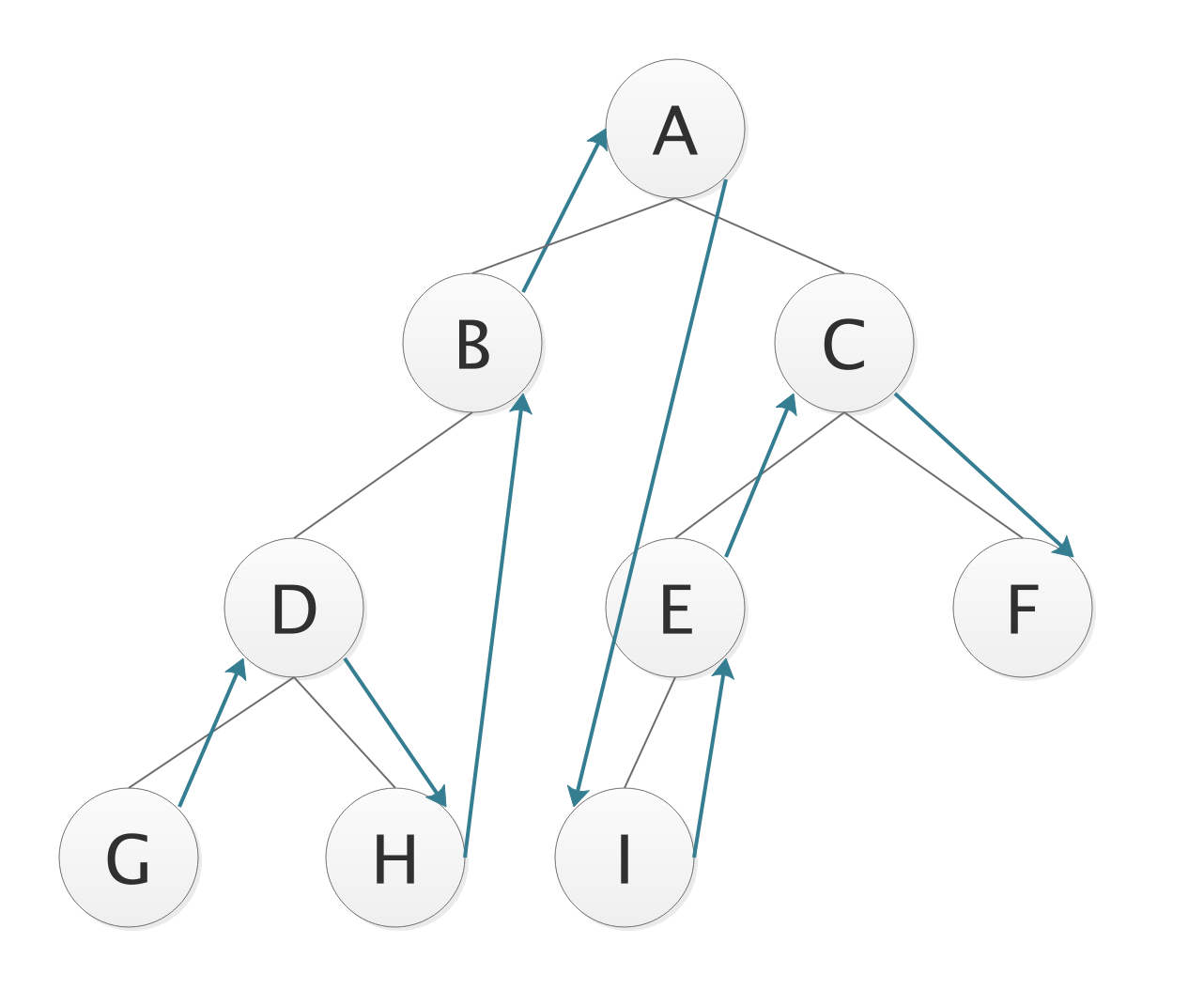
GDHB A EICF
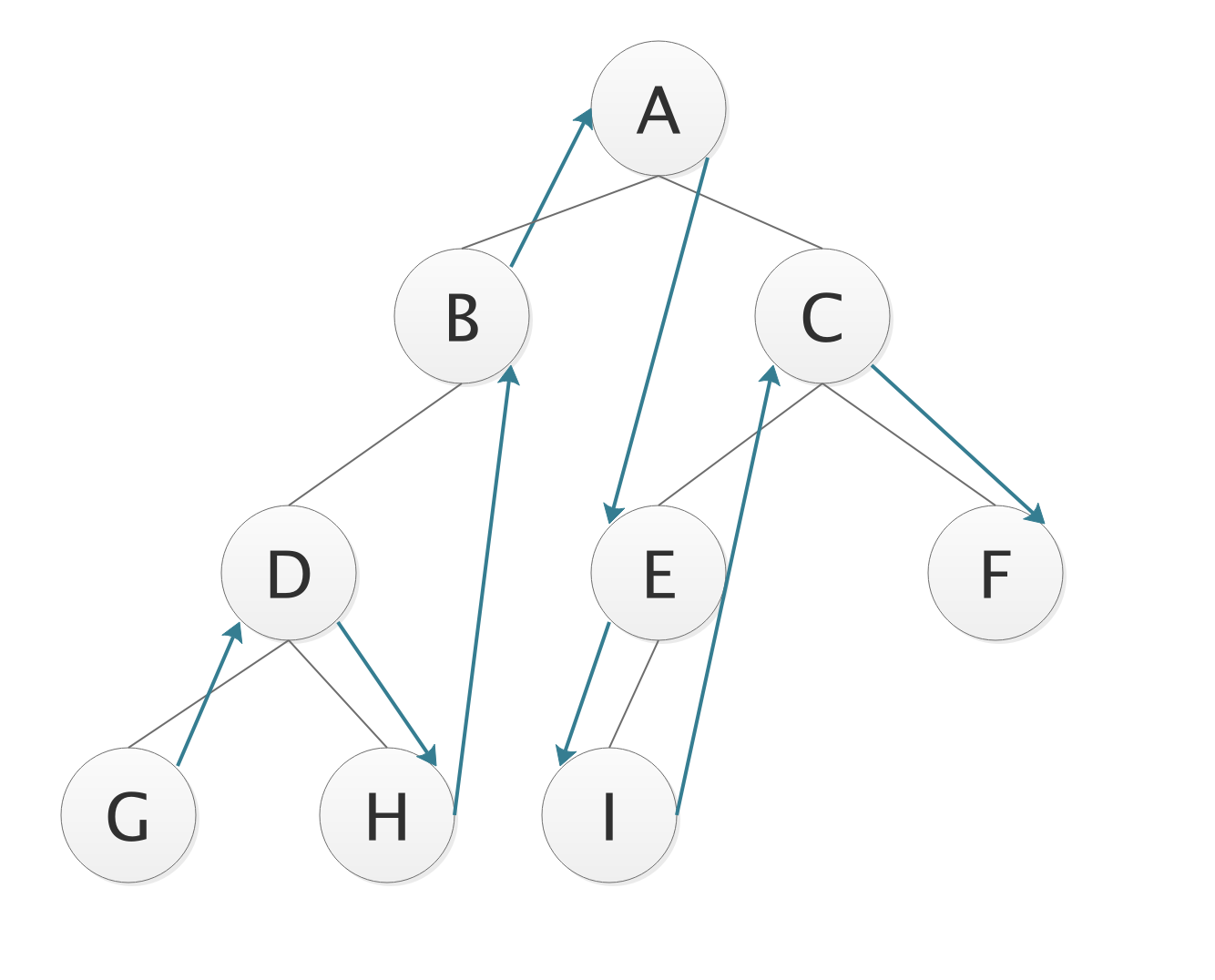
- 后序遍历LRD
- 先左子树,后右子树,再根结点;
- 每个子树内部依然是先左子树,后右子树,再根结点。递归遍历;
- 遍历序列;
GHDB IEFC A
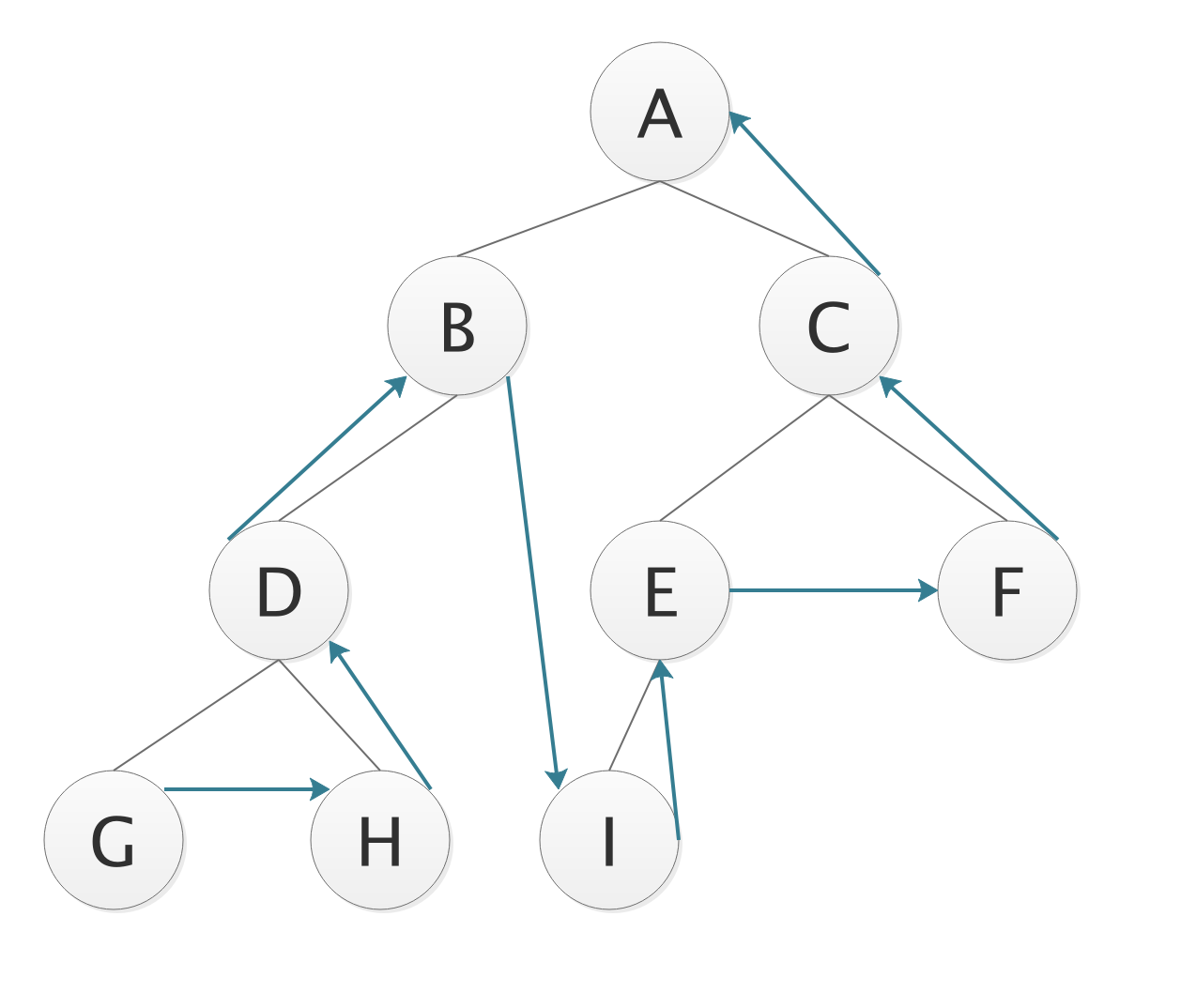
堆排序Heap Sort
- 堆Heap
- 堆是一个完全二叉树;
- 每个非叶子结点都要大于或者等于其左右孩子结点的值称为大顶堆;
- 每个非叶子结点都要小于或者等于其左右孩子结点的值称为小顶堆;
- 根结点一定是大顶堆中的最大值,一定是小顶堆中的最小值;
- 大顶堆
- 完全二叉树的每个非叶子结点都要大于或者等于其左右孩子结点的值称为大顶堆;
- 根结点一定是大顶堆中的最大值;
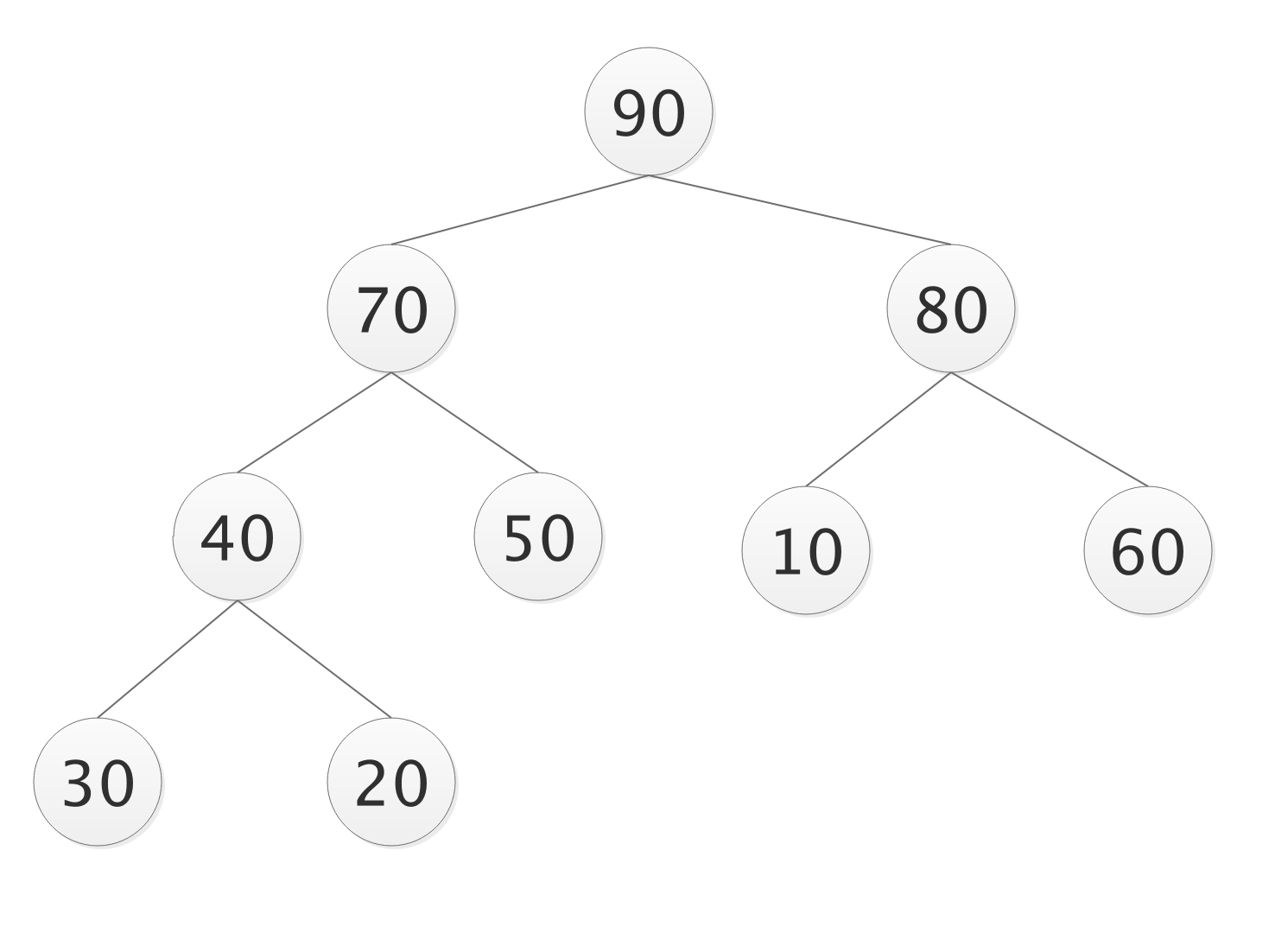
- 小顶堆
- 完全二叉树的每个非叶子结点都要小于或者等于其左右孩子结点的值称为小顶堆;
- 根结点一定是小顶堆的最小值;
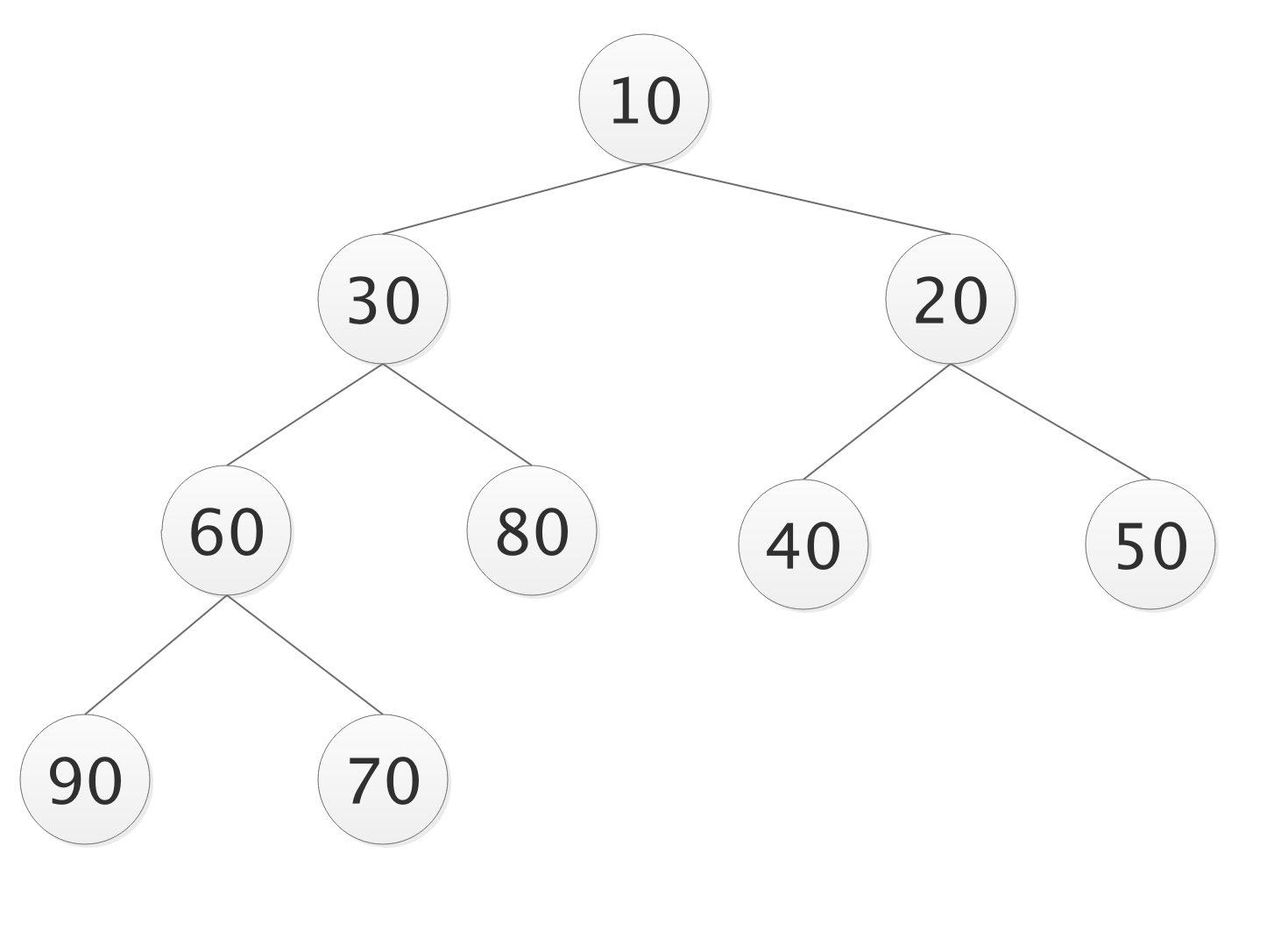
- 构建完全二叉树
- 待排序数字为 30,20,80,40,50,10,60,70,90;
- 构建一个完全二叉存放数据,并根据性质5对元素编号,放入顺序的数据结构中;
- 构建一个列表为[0,30,20,80,40,50,10,60,70,90]
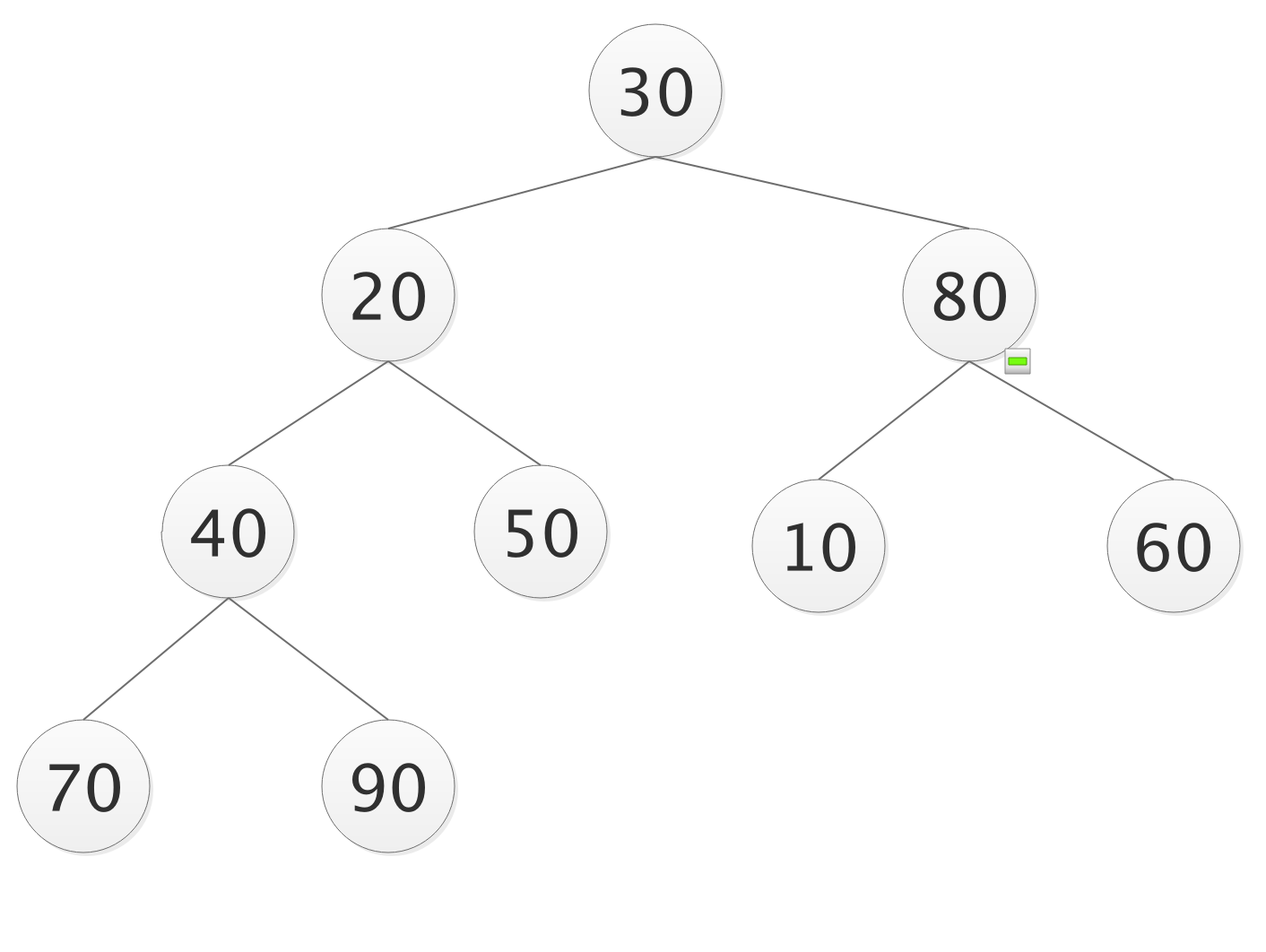
- 构建大顶堆—核心算法
- 度数为2的结点A, 如果它的左右孩子结点的最大值比它大的,将这个最大值和该结点交换;
- 度数为1的结点A, 如果它的左孩子的值在于它,则交换;
- 如果结点A被交换到新的位置,还需要和其孩子结点重复上面的过程;
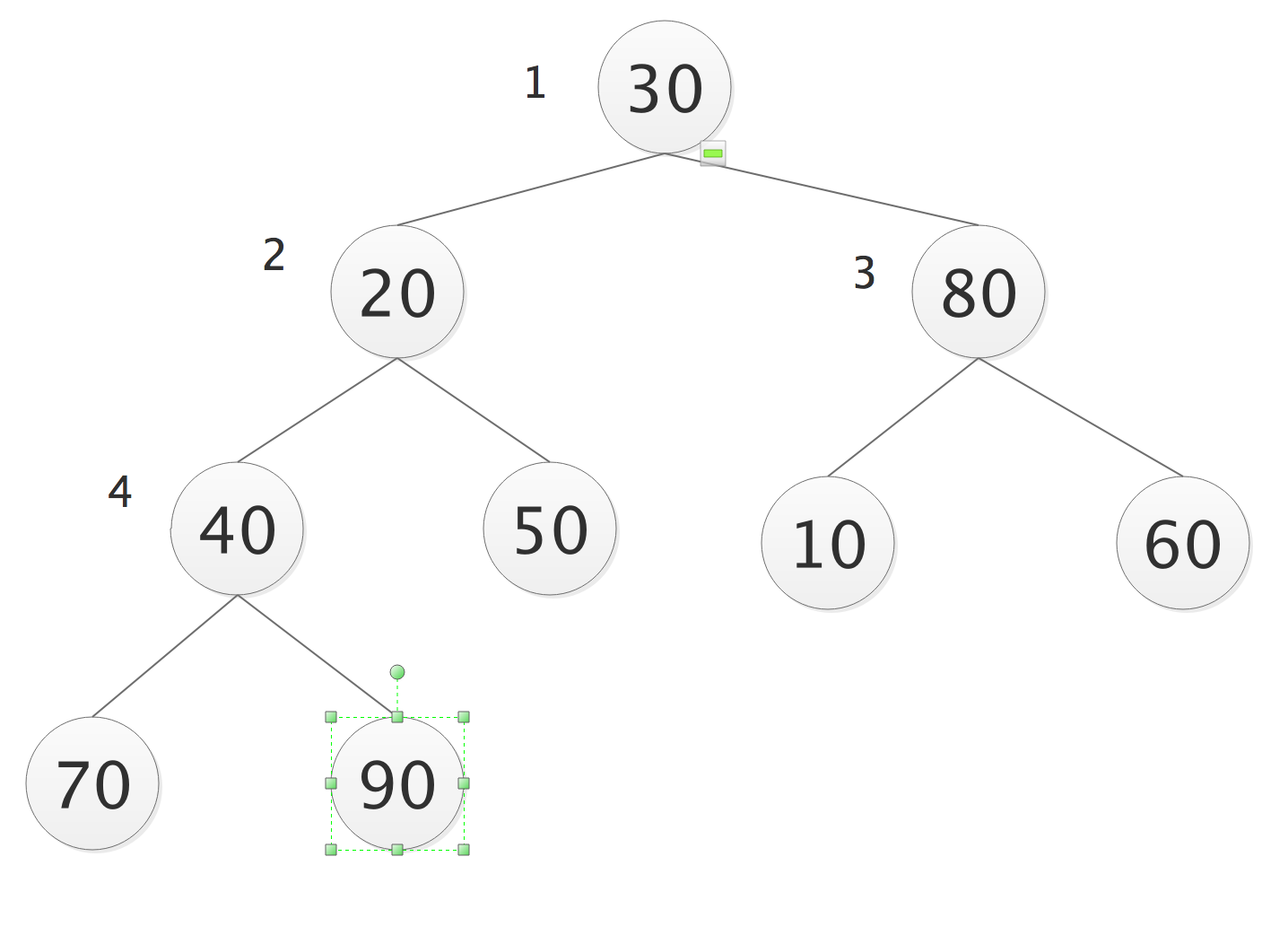
- 构建大顶堆—起点结点的选择;
- 从完全二叉树的最后一个结点的双亲结点开始,即最后一层的最右边叶子结点的父结点开始;
- 结点数为n,则起始结点的编号n//2
- 构建大顶堆—下一个结点的把选择
- 从起始结点开始向左找其同层结点,到头后再从上一层的最右边结开始继续向左逐个查找,下直到根结点;
大顶堆的目标
确保每个结点的都比左右右结点的值大;
排序
将大顶堆根结点这个最大值和最后一个叶子结点交换,那么最后一个叶子结点就是最大值,将这个叶子结点排除在待排序结点之后;
从根结点开始(新的结点),重新调整为大顶堆后,重复上一步;
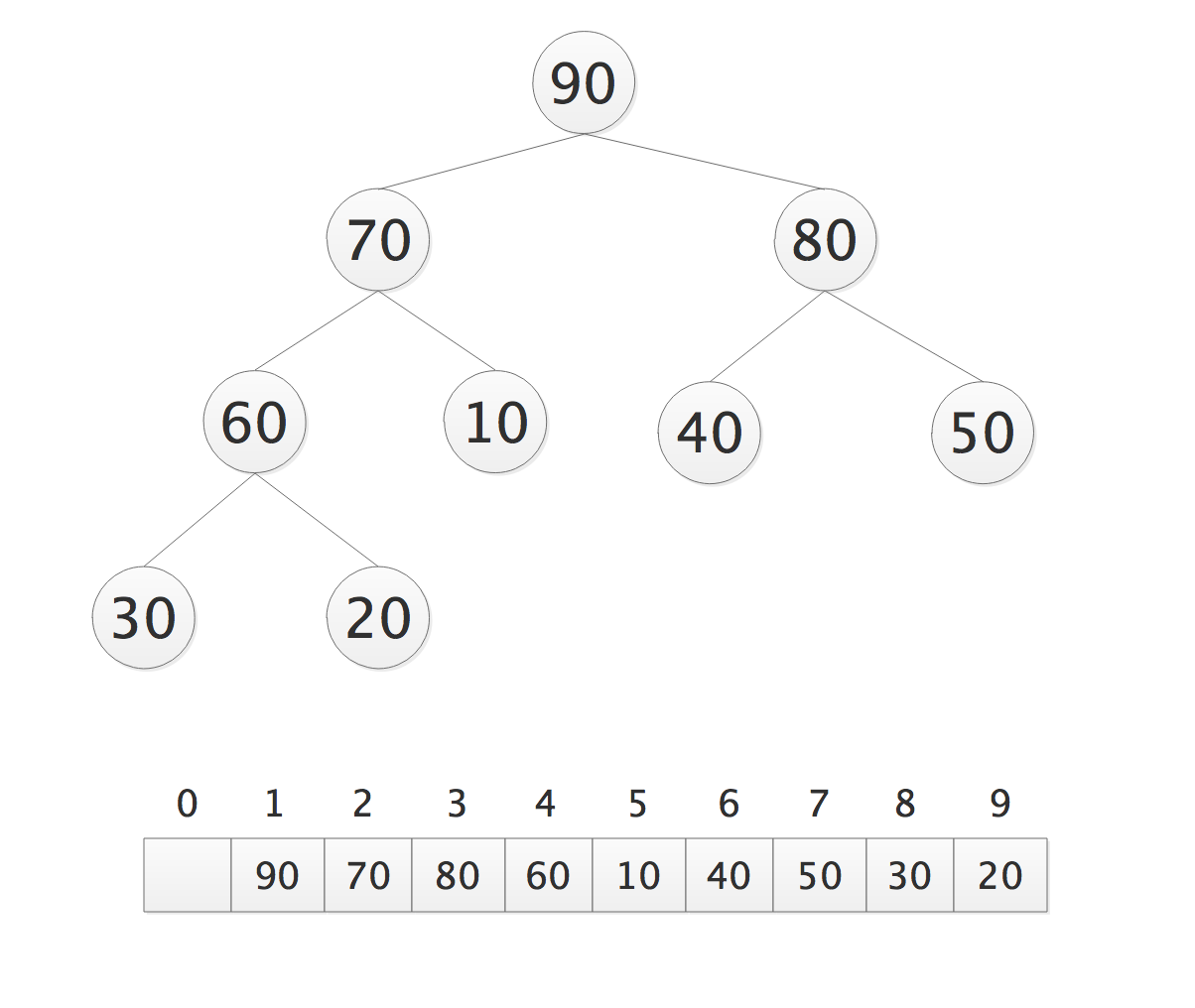
- 排序
- 堆顶和最后一个结点交换,并排除最后一个结点;
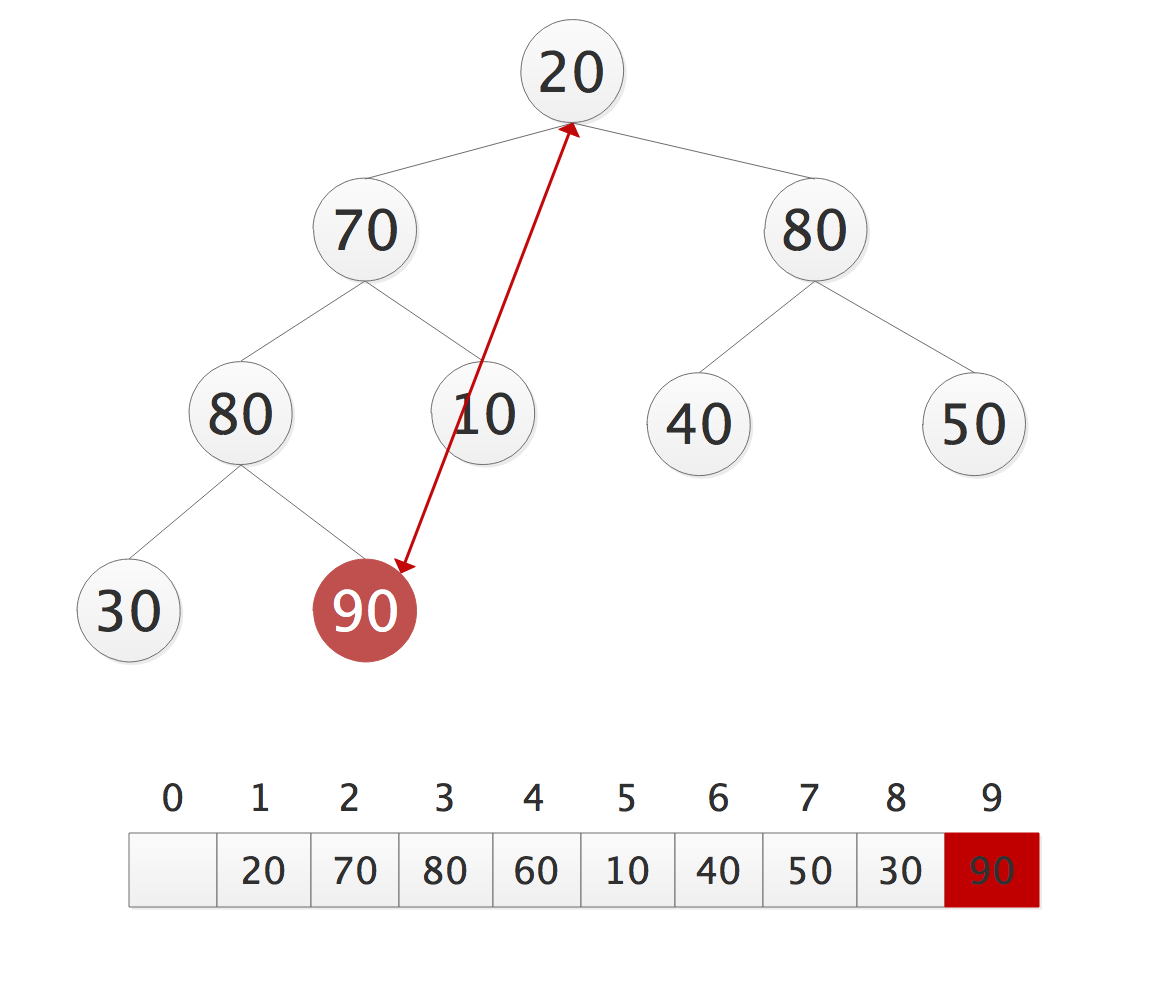
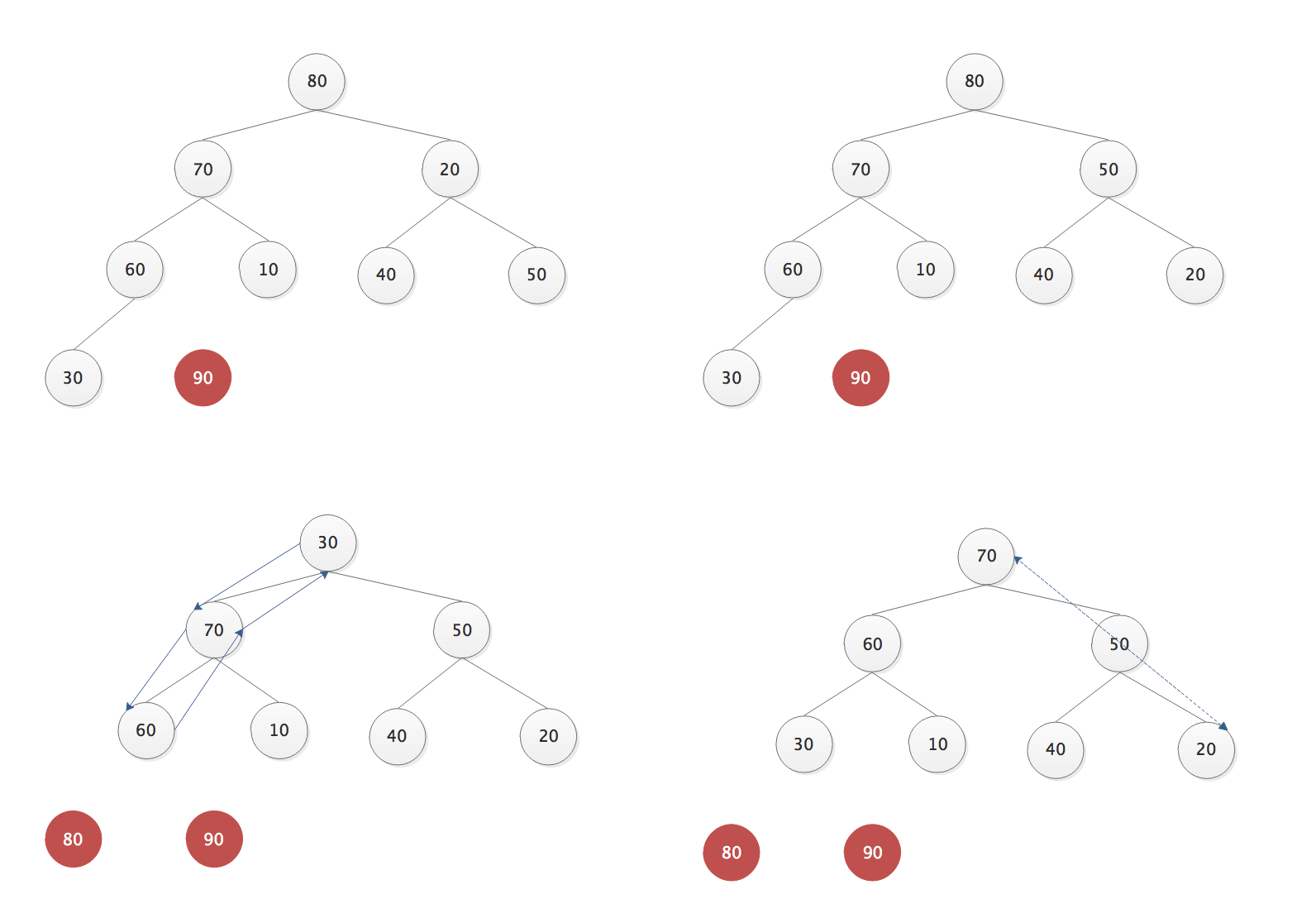
练习
打印一个树
origin = [30,20,80,40,50,10,60,70,90]
30
20 80
40 50 10 60
70 90
思路:
每一行取1个,第二行取2个,第三行取3个,以此类推;
投影来思考一个栅格系统;
代码实现
import math
def print_tree(array):
'''
前空格 元素间
1 7 0
2 3 7
3 1 3
4 0 1
'''
index = 1
depth = math.ceil(math.log2(len(array))) # 因为补0了,不然应该是math.ceil(math.log2(len(array)+1))
sep = ' '
for i in range(depth):
offset = 2 ** i
print(sep *(2 **(depth -i -1) -1),end = '')
line = array[index:index+offset]
for j,x in enumerate(line):
print("{:>{}}".format(x,len(sep)), end='')
interval =0 if i ==0 else 2**(depth -i) -1
if j < len(line) -1:
print(sep * interval,end='')
index += offset
print()
print_tree([0,30,20,80,40,50,10,60,70,90,22])
print_tree([0,30,20,80,40,50,10,60,70,90,22,33,44,55,66,77])
print_tree([0,30,20,80,40,50,10,60,70,90,22,33,44,55,66,77,88,99])
#输出
30
20 80
40 50 10 60
70 90 22
30
20 80
40 50 10 60
70 90 22 33 44 55 66 77
30
20 80
40 50 10 60
70 90 22 33 44 55 66 77
88 99
堆调整
- 核心算法
对于堆排序的核心算法就是堆结点的调整
- 度数为2的结点A,如果它的左右孩子结点的最大值比它大的,将这个最大值和该结点交换;
- 度数为1的结点A,如果它的左右孩子的值大于它,则交换;
- 如果结点A被交换到新的位置,还需要和其孩子 结点重复上面的过程;
import math
def print_tree(array):
'''
前空格 元素间
1 7 0
2 3 7
3 1 3
4 0 1
'''
index = 1
depth = math.ceil(math.log2(len(array))) # 因为补0了,不然应该是math.ceil(math.log2(len(array)+1))
sep = ' '
for i in range(depth):
offset = 2 ** i
print(sep *(2 **(depth -i -1) -1),end = '')
line = array[index:index+offset]
for j,x in enumerate(line):
print("{:>{}}".format(x,len(sep)), end='')
interval =0 if i ==0 else 2**(depth -i) -1
if j < len(line) -1:
print(sep * interval,end='')
index += offset
print()
# Heap Sort
# 为了和编码对应,增加一个无用的0在首位
# origin = [0,50,10,90,30,70,40,80,60,20]
origin = [0,30,20,80,40,50,10,60,70,90]
total = len(origin) -1 # 初始待排序元素个数,即n
# print_tree([0,30,20,80,40,50,10,60,70,90,22])
# print_tree([0,30,20,80,40,50,10,60,70,90,22,33,44,55,66,77])
# print_tree([0,30,20,80,40,50,10,60,70,90,22,33,44,55,66,77,88,99])
def heap_adjust(n, i, array: list):
'''
调整当前结点(核心算法)
调整的结点的起点在n//2,保证所有调整的结点都有孩子结点
:param n: 待比较数个数
:param i: 当前结点的下标
:param array: 待排序数据
:return: None
'''
while 2 * i <=n:
#孩子结点判断2i为左孩子,2i+1为右孩子
lchile_index = 2 * i
max_child_index = lchile_index # n=2i
if n > lchile_index and array[lchile_index +1 ]> array[lchile_index]:# n>2i说明还有右孩子
max_child_index = lchile_index +1
# 和子树的根结点比较
if array[max_child_index] > array[i]:
array[i],array[max_child_index] = array[max_child_index],array[i]
i = max_child_index # 被交换后,需要判断是否还需要调整
else:
break
#print_tree(array)
heap_adjust(total,total//2,origin)
print(origin)
print_tree((origin))
到目前为止也只是解决了单个结点的调整,下面要使用循环来今次解决比起始结点编号小的结点;
构建大顶堆
起点的选择
从最下层最右叶子结点的父结点开始;
由于构造了一个前置的0,所以编号和列表索引正好重合;下一个结点
按照二叉树性质5编号的结点,从起点开始找编号逐个递减的结点,直到编号1;
import math
def print_tree(array):
'''
前空格 元素间
1 7 0
2 3 7
3 1 3
4 0 1
'''
index = 1
depth = math.ceil(math.log2(len(array))) # 因为补0了,不然应该是math.ceil(math.log2(len(array)+1))
sep = ' '
for i in range(depth):
offset = 2 ** i
print(sep *(2 **(depth -i -1) -1),end = '')
line = array[index:index+offset]
for j,x in enumerate(line):
print("{:>{}}".format(x,len(sep)), end='')
interval =0 if i ==0 else 2**(depth -i) -1
if j < len(line) -1:
print(sep * interval,end='')
index += offset
print()
# Heap Sort
# 为了和编码对应,增加一个无用的0在首位
# origin = [0,50,10,90,30,70,40,80,60,20]
origin = [0,30,20,80,40,50,10,60,70,90]
total = len(origin) -1 # 初始待排序元素个数,即n
# print_tree([0,30,20,80,40,50,10,60,70,90,22])
# print_tree([0,30,20,80,40,50,10,60,70,90,22,33,44,55,66,77])
# print_tree([0,30,20,80,40,50,10,60,70,90,22,33,44,55,66,77,88,99])
def heap_adjust(n, i, array: list):
'''
调整当前结点(核心算法)
调整的结点的起点在n//2,保证所有调整的结点都有孩子结点
:param n: 待比较数个数
:param i: 当前结点的下标
:param array: 待排序数据
:return: None
'''
while 2 * i <=n:
#孩子结点判断2i为左孩子,2i+1为右孩子
lchile_index = 2 * i
max_child_index = lchile_index # n=2i
if n > lchile_index and array[lchile_index +1 ]> array[lchile_index]:# n>2i说明还有右孩子
max_child_index = lchile_index +1
# 和子树的根结点比较
if array[max_child_index] > array[i]:
array[i],array[max_child_index] = array[max_child_index],array[i]
i = max_child_index # 被交换后,需要判断是否还需要调整
else:
break
#print_tree(array)
# 构建大顶堆、大根堆
def max_heap(total,array:list):
for i in range(total//2,0,-1):
heap_adjust(total,i,array)
return array
print_tree(origin)
print_tree(max_heap(total,origin))
# 输出
30
20 80
40 50 10 60
70 90
90
70 80
40 50 10 60
20 30
结论,最大的一定在第一层,第二层一定有一个次大的;
排序
- 每次都要让堆顶的元素和最后一个结点交换,然后排除最后一些元素,开成一个新的被破坏的堆;
- 让它重新调整,调整后,堆顶一定是最大的元素;
- 再次重复第1、2步直剩余一个元素;
def sort(total,array:list):
while total > 1:
array[1], array[total] = array[total],array[1] #堆顶和最后一个结点交换
total -=1
heap_adjust(total,1,array)
return array
print_tree(sort(total,origin))
改进
def sort(total, array:list):
while total >1:
array[1],array[total] = array[total],array[1]# 堆顶和最后一个结点交换
total -= 1
if total == 2 and array[total] >= array[total-1]:
break
heap_adjust(total,1,array)
return array
print_tree(origin)
print_tree(sort(total,origin))
总结堆排序
- 是利用堆性质的一种选择排序,在堆 顶选出最大值或者最小值;
时间复杂度;
- 堆排序的时间复杂度为O(nlogn)
- 由于堆排序对原始记录的排序状态并不敏感,因hxpx无论是最好、最坏和平均时间复杂度均为O(nlogn)
nlogn 可以大大提高排序的效率;
空间复杂度
- 只是使用了一个交换用的空间,空间复杂度就是O(1)
稳定性
- 不稳定的排序算法;
格言
天下事无所为而成者极少,有所贪有所利而成者居其半,有所激有所逼而成者居其半;
百端拂逆之时,亦只有逆来顺受之法;
“所谓’好汉打掉牙和血吞’ 真处离境之良法也;